Tensor-Based Operator Assembly and Evaluation

Overview

The high performance (HPC) versions of the example codes in the miniapps/performance directory use a set of templated classes to efficiently implement the inner-most portion ($B^T D B$) of the fundamental finite element (FE) operator decomposition:

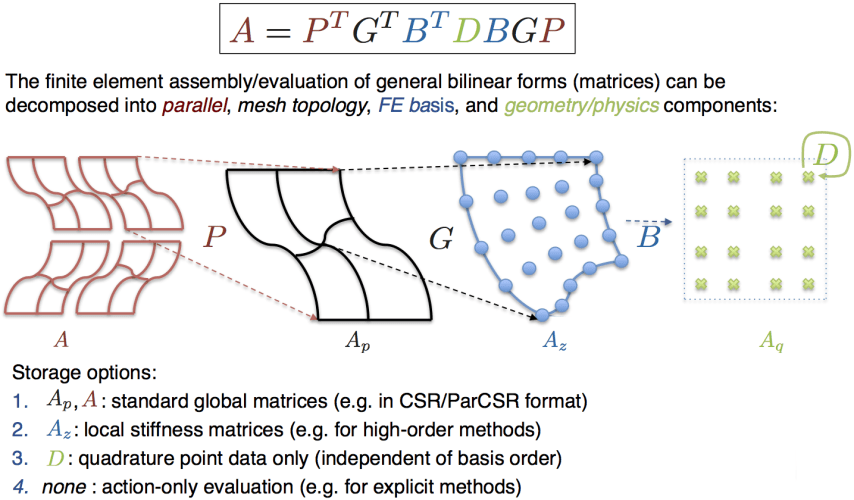
We take advantage of the tensor-product structure of both the finite element basis and the quadrature rule to efficiently apply the action of $B$ without necessarily computing its entries. This is generally know as sum factorization. In the case where we pre-compute and store the $D$ matrix, we call the algorithm partial assembly.

Template implementation

Below is a short description of the header files that are part of the initial reference implementation of the tensor-based finite element assembly and evaluation algorithms.

config/tconfig.hpp

Configuration macros including the specification of the template blocking size (currently used in the matrix-matrix multiply).

general/tassign.hpp

Helper templated function to allow single implementation of multiple assignment operations on tensor entries.

linalg/tlayout.hpp

Classes describing fixed size tensor layouts. Implemented are standard strided layouts for 1D/2D/3D/4D tensors. Layouts support reshape and sub-tensor operations independent of the actual data storage.

This header also contains another set of "vector layout" classes for converting scalar data indices into multi-component (vector) data indices. They are used to describe the layout of vector GridFunctions on global degrees of freedom (similar to the Ordering class). In the FE operator decomposition, these classes are used by the templated *_FiniteElementSpace classes (see fem/tfespace.hpp below) to implement the actions of $G$ and $G^T$ in the case of vector (multi-component) input and/or output fields.

linalg/tmatrix.hpp

Small matrix operations, defined by specializations: determinant, adjugate, etc. Matrix-matrix multiply, C = A.B, simple and blocked version.

linalg/ttensor.hpp

Fixed-size container classes TVector, TMatrix, TTensor3, TTensor4 for 1D/2D/3D/4D tensors stored in column-major layout. Element-wise tensor operations: A {=,+=,*=} scalar; A {=,+=,*=} B. The latter allows different input and output layouts. With suitable layouts this can be used to permute (transpose) tensors, extract sub-tensors, etc. The tensor contraction/product operations:

• Mult_1_2: $C_{i,j,k} = \sum_s A_{s,j} B_{i,s,k}$
• Mult_2_1: $C_{i,j,k} = \sum_s A_{i,s} B_{s,j,k}$
• TensorAssemble: $C_{i,k,j,l} = \sum_s A_{s,i} A_{s,j} B_{k,s,l}~~$ and $~~D_{i,k,j,l} = \sum_s A_{i,s} B_{s,j} C_{k,s,l}$
• TensorProduct: $C_{i,j,k,l} = A_{i,j,k} B_{j,l}$

mesh/tmesh.hpp

The Mesh object templated by the finite element space and layout of the nodes. Provides MatchesGeometry() and MatchesNodes() functions to verify if compiled and runtime mesh agree.

fem/tintrules.hpp

Quadrature rules templated by geometry (triangles, quads, etc.) and integration order.

fem/tfe.hpp

H1 and L2 finite elements templated by geometry and polynomial order.

fem/tfespace.hpp

Template *_FiniteElementSpace classes providing the mappings between global and local (element) degrees of freedom for H1 continuous and L2 discontinuous spaces. In the FE operator decomposition, these classes provide the element local action of $G$ (Extract methods) and $G^T$ (Assemble methods).

fem/tcoefficient.hpp

Templated versions of classes derived from the abstract class Coefficient. It encapsulates physical quantities like material properties, sources, boundary/initial conditions, etc. Its main functionality is to evaluate the coefficient at all quadrature points in an element, which is then used in the evaluation of the $D$ matrix.

fem/teltrans.hpp

Element transformation class, templated on a mesh type and an integration rule. It is constructed from a mesh (e.g. class TMesh) and shape evaluator (e.g. class ShapeEvaluator) objects. Allows computation of physical coordinates and Jacobian matrices corresponding to the reference integration points. The desired result (a combination of coordinates and/or Jacobian matrices at quadrature points, element attribute and/or element index) is specified through the template sub-class Result and stored in an object of the same type. The idea of this approach is to eliminate unnecessary evaluations if they are not needed. The need is determined based on what the particular "users" need. The "users" are the templated Coefficient and Kernel (see fem/tbilininteg.hpp below) classes which specify what they need through static constant boolean variables, e.g. uses_coordinates, uses_Jacobians, etc.

fem/tevaluator.hpp

Classes for evaluating FE basis, ShapeEvaluator, and finite element functions, FieldEvaluator, and their derivatives at quadrature points, templated by a finite element class and an integration rule class. These correspond to the $B$ and $BG$ matrices above. Quads and hexes use the tensor-product structure for fast evaluation.

fem/tbilininteg.hpp

Kernel classes (e.g. mass, diffusion) that represent the matrix $D$ from the above FE operator decomposition. These classes also specify the type of the local operator that needs to be applied before and after the $D$ matrix - these are the $B_{in}$ and $B^T_{out}$ matrices, respectively. The product $B^T_{out} D B_{in}$ is the local element matrix, which is the result when using the BilinearFormIntegrator classes. This specifications of the types are given by static constant boolean variables, e.g. in_values and out_values. The Kernel classes provide the following methods:

• Action: evaluate the action of $D$ without explicitly storing the partially assembled data; this is needed for matrix-free action.
• Assemble: evaluate the partially assembled data, $D$, which is kernel-specific: e.g., for mass, the data is one scalar per quadrature point; for diffusion, the data is one $d\times d$ matrix (in $d$-dimensions) per quadrature point.
• MultAssembled: perform the action of $D$ using the pre-computed partially assembled data.

fem/tbilinearform.hpp

Bilinear form operator, templated on the mesh, finite element space, integration rule and bilinear form integrator. Corresponds to the $A$ matrix above. Provides various assembly and evaluation schemes:

• MultUnassembled: matrix-free action using the mesh nodes and the input vector.
• Assemble, MultAssembled: partial assembly and operator action using the partially assembled data at quadrature points and the input vector.
• AssembleMatrix(DenseTensor &): assemble the local element matrices and store them as DenseTensor.
• AssembleMatrix(SparseMatrix &): assemble the operator in a global (CSR) SparseMatrix.
• AssembleBilinearForm(BilinearForm &): assemble element matrices and add them to the bilinear form.

miniapps/performance/makefile

By default make builds the example drivers with the compiler used to compile MFEM. If g++ was used, a pseudo-code dump file with the optimized code will be generated (option -fdump-tree-optimized-blocks). The g++ option --param max-completely-peel-times=3 prevents the compiler from unrolling innermost loops (of size greater than 3), allowing the compiler to vectorize them. Some options for optimization/vectorization with the clang compiler are also included.

miniapps/performance/ex*.cpp

High-performance templated versions of the corresponding examples/ex*.cpp example codes.