HowTo: Nonconforming and AMR meshes

The Mesh class provides basic element refinement capabilities:

• All elements may be refined uniformly with Mesh::UniformRefinement.
• Local refinement is supported, but only for simplex elements. The method Mesh::GeneralRefinement uses recursive bisection in this case.

These basic refinement methods preserve mesh conformity, i.e., no hanging nodes are created. This also means that quadrilaterals and hexahedra cannot be refined locally by the Mesh class.

For more advanced AMR, MFEM has the class NCMesh:

• Tensor product element refinement (quad, hex, prism) is supported, including anisotropic refinement. Hanging nodes are created and handled transparently.
• Triangles and tetrahedra use "red" (isotropic) refinement, also producing hanging nodes in this mode.
• Derefinement (coarsening) of previously refined elements is possible.
• In parallel, the mesh can be load balanced.

The user does not interact directly with the NCMesh class — it is created behind the scenes, and the Mesh class in nonconforming mode, continually updated to contain the finest elements of the refinement hierarchy, still serves as an interface for the user and other MFEM classes.

To switch to the nonconforming mode (or convert and existing conforming Mesh), you need to call EnsureNCMesh, typically at the beginning after loading the mesh:

Mesh *mesh = new Mesh(mesh_file, 1, 1);
mesh->EnsureNCMesh(true);

The boolean parameter, if true, forces simplex meshes to use nonconforming refinement (the default is false).

Nonconforming refinement

Once the Mesh is in nonconforming mode, you can simply call Mesh::GeneralRefinement to locally refine a subset of elements:

Array<int> refinement_list;
for (int i = 0; i < mesh->GetNE(); i++)
{
   if (/*element i refinement condition*/)
   {
      refinement_list.Append(i);
   }
}
mesh->GeneralRefinement(refinement_list);

The resulting hanging nodes will be treated transparently by the FiniteElementSpace and BilinearForm classes:

• FiniteElementSpace will internally construct a conforming interpolation matrix $P$, that when applied to a vector of unconstrained ("true") DOFs, will augment the vector with interpolated constrained DOFs.

• Once the linear system $Ax = b$ is assembled, BilinearForm::FormLinearSystem will eliminate constrained nodes by transforming the linear system to $P^TAPx = P^Tb$ (see ex1.cpp).

• After the reduced system is solved, the conforming solution on all nodes is recovered as $y = P x$ with BilinearForm::RecoverFEMSolution.

Limiting the level of hanging nodes

By default, MFEM does not limit the sizes of adjacent elements in nonconforming meshes. For some applications, it may be necessary to ensure that the refinement level of neighboring elements differs by at most one, for example.

The optional parameter nc_limit of Mesh::GeneralRefinement can be used to control the maximum level of nonconformity. If nc_limit is greater than zero, the method will automatically perform additional refinements to make sure the difference of refinement levels of adjacent elements is at most nc_limit.

Anisotropic refinement

Uniquely, MFEM offers the capability to perform anisotropic refinement of tensor product elements in both 2D and 3D. The method Mesh::GeneralRefinement has two overloads, one taking a simple list of elements to refine (as seen above), and the other taking a list of struct Refinement { int index; char ref_type; }, where one can specify a refinement type for each element in the list:

Array<Refinement> refinement_list;
refinement_list.Append(Refinement(0, 2));
refinement_list.Append(Refinement(1, 4));
mesh->GeneralRefinement(refinement_list);

This code will refine the first element (index 0) of the mesh in the Y direction only (provided it is a quad or hex element) and the second element (index 1) in the Z direction only. The directions are assumed in the element reference coordinates and are encoded as follows:

Note that the refinement type is encoded as a 3-bit number, where bits 0, 1, 2 correspond to the X, Y, Z directions, respectively. Other element geometries allow fewer but similar refinement types: triangle (3), quadrilateral (1, 2, 3), tetrahedron (7), prism (3, 4, 7).

In 3D meshes with anisotropic refinements it is easy to arrive at conflicting situations, where the refined faces of adjacent elements are not subsets of each other. For example, running the above code on a mesh with two hexahedra adjacent in the X direction will create an interface that cannot be constrained correctly. In such cases, MFEM will automatically adjust one side of the interface with additional refinements (called forced refinements) to ensure that the mesh remains a valid FEM mesh. In pathological cases the forced refinements may propagate. Using a reasonable nc_limit may reduce this effect. Nevertheless, a valid mesh is produced in all cases.

Derefinement

To coarsen elements, use the method Mesh::DerefineByError. The interface is different from refinement, because it is not possible to coarsen arbitrary groups of fine elements: it is only possible to reintroduce previously existing coarse elements by undoing their refinement (hence the term "derefinement").

Since one cannot supply the indices of elements that no longer exist in the Mesh class (the refinement trees are kept internal to NCMesh), the method DerefineByError works indirectly by taking an array of "error" values corresponding to each element of the current Mesh. If the sum of error values of the children of some coarse element is below a supplied threshold, the children are removed and the coarse element is restored in Mesh.

If the user specifies a nonzero nc_limit, care is taken not to derefine elements that are needed to keep the required level of nonconformity.

Note: derefinement is not yet supported for meshes containing 3D anisotropic refinements.

Parallel nonconforming meshes

Just as the Mesh class has a parallel counterpart (ParMesh), so does the NCMesh class have a parallel descendant: ParNCMesh. The parallel class is again kept internal and the user can continue to interact with the standard ParMesh class (see examples ex1p, ex6p and ex15p).

The refinement hierarchy in parallel NC mode is fully distributed and scales to billions of elements and hundreds of thousands of MPI tasks. Ghost elements are automatically tracked by the ParNCMesh class, so that a parallel conforming interpolation matrix can be constructed by ParFiniteElementSpace. Depending on the assembly level, ParBilinearForm will either explicitly assemble the parallel $P^TAP$ system using the Hypre library, or the action of the $P$ matrix will be applied during solver iterations.

Parallel refinement is still done through Mesh::GeneralRefinement inherited by the ParMesh class. The method takes local element indices and works the same as in serial. All parallel concerns such as keeping the ghost layers synchronized are handled internally in ParNCMesh.

Note: parallel anisotropic refinement of 3D meshes is not supported yet.

After each mesh operation (refinement, derefinement, load balancing) the ParMesh is updated to reflect the current parallel mesh state (minus the ghost elements, which are not exported to ParMesh). Communication groups, used in conforming mode for reductions/broadcasts over parallel solution vectors, are approximated in the NC mode as if the mesh was cut along the nonconforming interfaces.

Load balancing

In conforming mode, a serial Mesh can only be partitioned statically (with METIS) when constructing a ParMesh. In nonconforming mode, the internal ParNCMesh class is capable of load balancing the distributed mesh at any time. This functionality is available to the user through ParMesh::Rebalance (see ex6p and ex15p).

The dynamic load balancing algorithm is based on partitioning a space-filling curve (SFC) that naturally arises when traversing the distributed refinement trees. Compared to spectral partitioners like METIS the partitions are not as high quality but the process is extremely fast and scales to hundreds of thousands of processors.

For best results with SFC-based partitioning, one condition has to be met: the elements of the coarse Mesh from which the ParMesh is constructed need to be ordered, ideally as a sequence of face-neighbors. This makes it possible for ParNCMesh to order the leaves of all refinement trees into a global linear sequence, which when equipartitioned should produce compact (albeit not minimal surface) mesh partitions.

Take for example a coarse mesh produced by the polar-nc miniapp. Except for two discontinuities, the elements are mostly ordered as a sequence of face-neighbors:

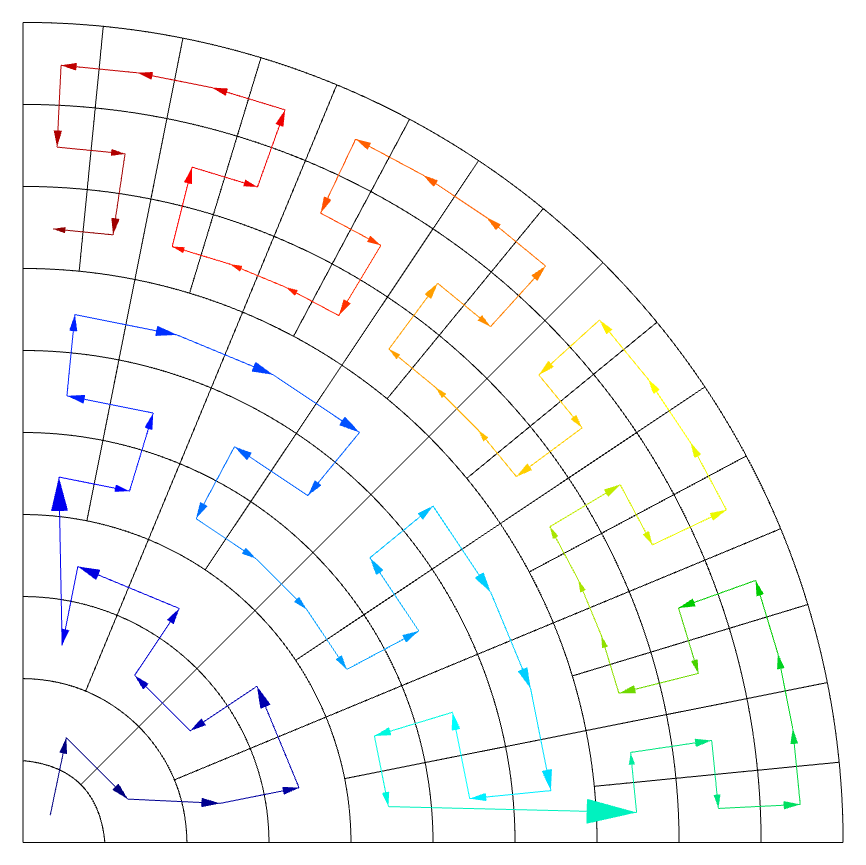
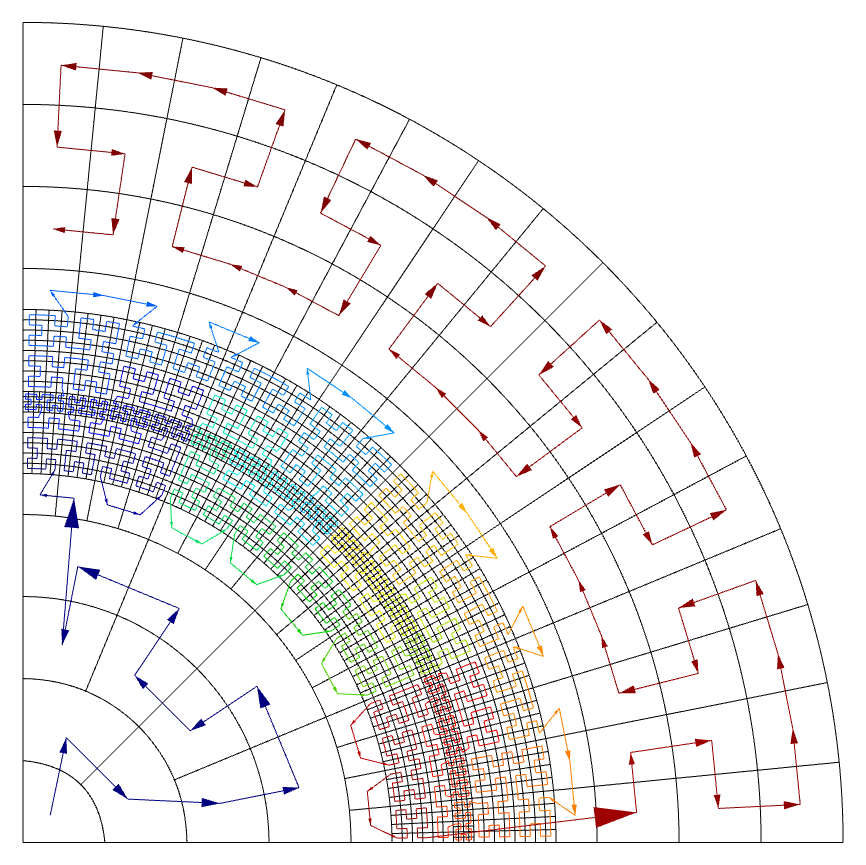
When we start refining elements (in both serial and parallel), MFEM will try to keep the space-filling curve continuous by inserting local Hilbert curves in the refined areas (press Ctrl+O in GLVis to visualize the ordering curve):

In a parallel computation, the global curve is then used for fast assignment of elements to MPI ranks. In the following run of ex15p, each processor is assigned the same number of elements (+/- one element). Note that the last partition is discontinuous due to a jump in ordering in the coarse mesh. This only affects the efficiency of MPI communication — the numerical results will be the same regardless of the partitioning.

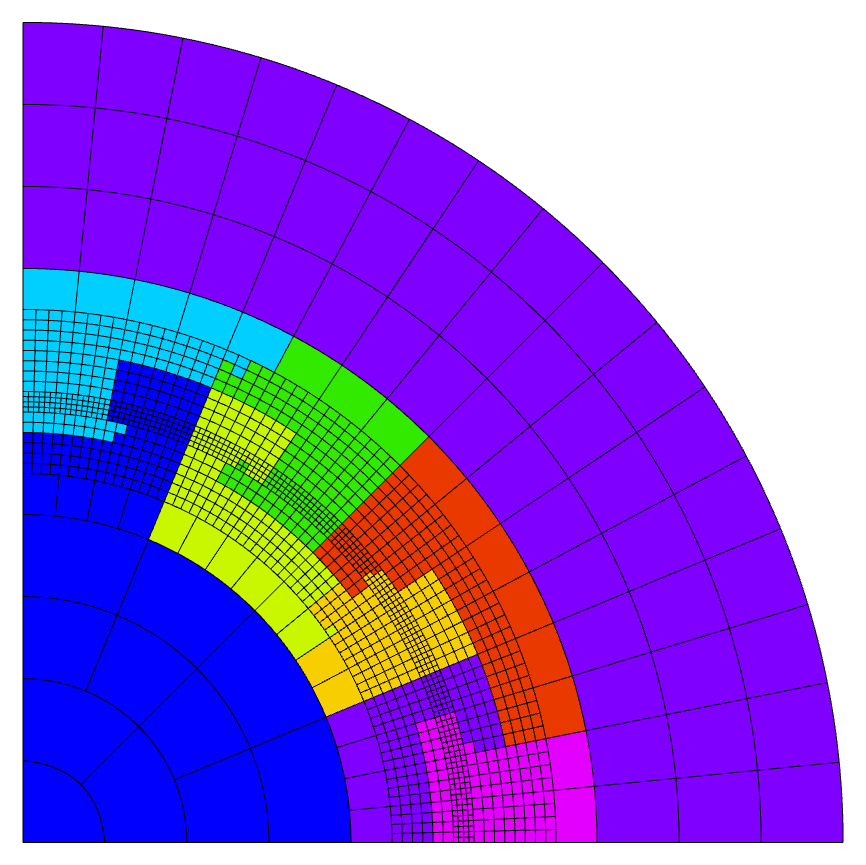
MFEM provides several methods to help with mesh ordering:

• Procedurally generated rectangular grids (Mesh::MakeCartesian2D, Mesh::MakeCartesian3D and also MFEM INLINE mesh v1.0 files) are by default ordered along a pseudo-Hilbert curve. Note that even grid dimensions are recommended, as explained here.

• General unstructured meshes may be ordered by a spatial sort algorithm (Mesh::GetHilbertElementOrdering). This is a fast method that will leave a number of jumps in complex meshes, but it is still highly recommended over not ordering the mesh at all.

• High-quality orderings of general meshes can be obtained with the Gecko library, now included directly in MFEM and available as Mesh::GetGeckoElementOrdering. The optimization algorithm used is more costly than a simple spatial sort, but it should produce better orderings for meshes with complex geometries. Beware the exponential cost of increasing the window parameter. Large meshes should probably be ordered in a preprocessing step (you may use the mesh-explorer miniapp for that).

Nonconforming mesh I/O

Nonconforming meshes have their own file format MFEM NC mesh v1.0, which supports all the additional internal structures (refinement trees, hanging nodes, etc.) and works for both serial and parallel NC meshes.

The method ParMesh::ParPrint will automatically choose the right format and can be used to save and restart an AMR computation, as demonstrated in example ex6p.

ParMesh::ParPrint should not be confused with the method ParMesh::Print, an analog of Mesh::Print, which is only suitable for visualization, as it uses the serial MFEM mesh v1.0 format and only adds the parallel shared faces to the output.