Solvers and Scalability

45 minutes intermediate

MFEM is designed to be highly scalable and efficient on a wide variety of platforms: from laptops to GPU-accelerated supercomputers. The solvers described in this lesson play a critical role in this parallel scalability.

  Scalable algebraic multigrid preconditioners from hypre

MFEM comes with a large number of example codes that demonstrate different physical applications, finite element discretizations, and linear solvers:

• Example 1 solves a Poisson problem,
• Example 2 solves a linear elasticity problem,
• Example 3 solves a definite Maxwell (electromagnetics) problem, and
• Example 4 solves grad-div diffusion problem.

The parallel versions of these examples (ex1p, ex2p, ex3p, and ex4p) each use suitable algebraic multigrid (AMG) preconditioners from the hypre solvers library. We describe sample runs with each of these examples in more details below.

  Example 1: Poisson problem and AMG

• First, make sure you are in the examples subdirectory: cd ~/mfem/examples

• Build the parallel version of Example 1: make ex1p

• Run the parallel version of Example 1, solving a Poisson problem: ./ex1p

• After forming the linear system, MFEM uses hypre to construct and apply an AMG preconditioner. Details of the AMG preconditioner are provided in the example output under the headers BoomerAMG SETUP PARAMETERS and BoomerAMG SOLVER PARAMETERS.

• Click here to view the terminal output

  

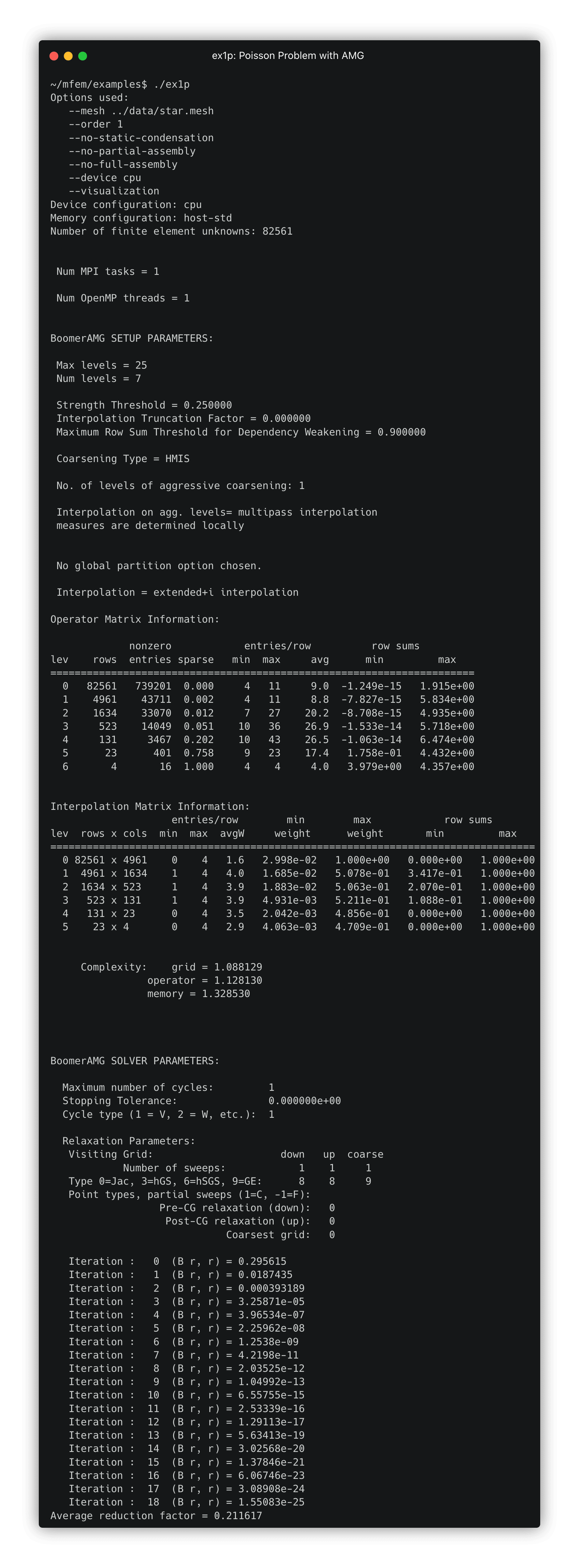
• A key feature of AMG methods is their scalability: with default options, convergence is achieved in only 18 conjugate gradient iterations.

• Let's see what happens if we increase the mesh refinement. Edit ex1p.cpp changing line 153 as follows:

  @@ -150,7 +150,7 @@ int main(int argc, char *argv[])
  ParMesh pmesh(MPI_COMM_WORLD, mesh);
  mesh.Clear();
  {
  -      int par_ref_levels = 2;
  +      int par_ref_levels = 3;
     for (int l = 0; l < par_ref_levels; l++)
     {
        pmesh.UniformRefinement();
  

• This adds one additional level of refinement, making the problem roughly 4 times as large in 2D, or 8 times as large in 3D.

• Rebuild the example (make ex1p) and re-run it: ./ex1p

• Although the number of unknowns for this problem has increased by roughly 4x, the iteration count remains at 18 due to the scalability of the AMG preconditioner.

• Let's now try a 3D problem. For that, we just need to choose a 3D mesh using the -m or --mesh command line argument.

• Because these problems are more computationally expensive, let's first reduce the refinement level, setting int par_ref_levels = 1; in the ex1p.cpp source code.

• Rebuild the example (make ex1p) and re-run it using the three-dimensional Fichera mesh: ./ex1p -m ../data/fichera.mesh. Convergence is attained in only 16 iterations.

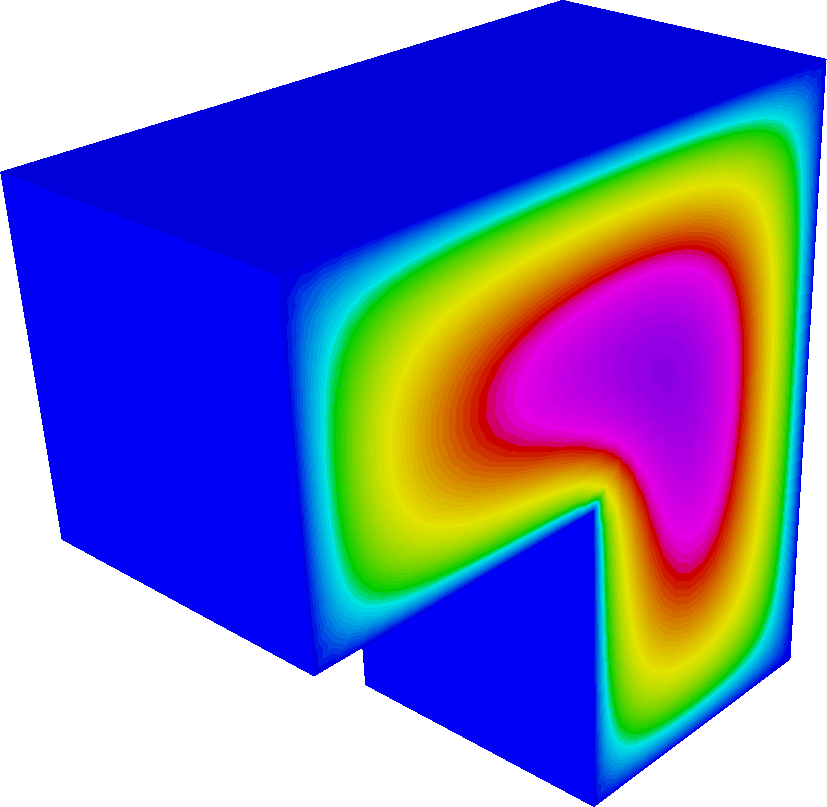
• Finally, let's take a look at the parallel scalability of the solvers:

  • Increase the refinement level: int par_ref_levels = 2;
  • Recompile: make ex1p
  • Now run the 3D example on 8 cores: mpirun -np 8 ./ex1p -m ../data/fichera.mesh
  • This is an example of a weak scaling test: the problem size and the number of processors are both increased by a factor of 8.
  • Because the PCG iteration counts remain roughly constant, the total time to solution should remain roughly fixed (minus some overhead and communication cost), even though we are solving a problem that is 8 times larger.

  Example 2: Linear Elasticity

• This example demonstrates solving a linear elasticity cantilever beam problem with different materials.

• This example is designed to work with any of the "beam" meshes provided by MFEM. Run ls ../data | grep beam to list the available 2D and 3D meshes: beam-hex-nurbs.mesh, beam-hex.mesh, beam-hex.vtk, beam-quad-amr.mesh, beam-quad-nurbs.mesh, beam-quad.mesh, beam-quad.vtk, beam-tet.mesh, beam-tet.vtk, beam-tri.mesh, beam-tri.vtk, beam-wedge.mesh, and beam-wedge.vtk.

• The elements and boundaries of these meshes are assigned attributes/materials suitable for the cantilever problem:

                         +----------+----------+
            boundary --->| material | material |<--- boundary
            attribute 1  |    1     |    2     |     attribute 2
            (fixed)      +----------+----------+     (pull down)

• Build the example with make ex2p.

• Try running ./ex2p in the terminal to run a 2D elasticity problem.

• As in Example 1, the linear system is solved using AMG.

• For this example, two types of AMG solvers can be used:

  1. A special version of AMG designed specifically for elasticity (see this paper).

  2. AMG for systems.

• To enable the special elasticity AMG, add the flag -elast to the command line, otherwise, AMG for systems will be used. For example: ./ex2p -elast.

• The polynomial degree (order) can be changed with the --order command line argument (-o for short). For example: ./ex2p -o 2. By default, low-order $(p=1)$ elements are used.

• Additionally, static condensation can be used to eliminate interior high-order degrees of freedom and obtain a smaller system. For --order 1, this has no effect. For higher-order problems, static condensation can improve efficiency.

• In this example, as before, the mesh refinement level can be controlled in the source code through par_ref_levels.

• Running with more than one MPI rank will partition the mesh and run the problem in parallel. Here is a sample 3D run: mpirun -np 8 ./ex2p -m ../data/beam-hex.mesh

• Try experimenting with different discretization, solver, and parallelization options.

  Examples 3 and 4: the de Rham Complex

• The next two examples demonstrate the use of vector finite element spaces.

  • Example 3 solves an electromagnetics problem using $H(\mathrm{curl})$ finite elements.

  • Example 4 solves a grad-div problem using $H(\mathrm{div})$ finite elements.

• Standard multigrid methods don't always work well for these problems, so we need specialized solvers! (See here for a paper on this topic.)

• For $H(\mathrm{curl})$ problems, we use the AMS solver from hypre.

• For $H(\mathrm{div})$ problems, we either use the ADS solver from hypre or a special hybridization solver. A recent saddle-point $H(\mathrm{div})$ solver is also available in the miniapps/hdiv-linear-solver directory. See this paper for more details.

• Try experimenting with different options to get a feel for the performance of the discretizations and solvers:

  • Change the mesh (2D or 3D) using the --mesh (-m) command line argument. For example: mpirun -np 16 ex3p -m ../data/beam-hex.mesh.

  • Change the polynomial degree using the --order (-o) command line argument. For example: mpirun -np 32 ex4p -m ../data/square-disc-nurbs.mesh -o 3.

  • Run problems in parallel using mpirun.

  • For ex4p, enable hybridization using the -hb flag. For example: mpirun -np 48 ex4p -m ../data/star-surf.mesh -o 3 -hb.

  MFEM's native Multigrid solver

• The previous examples (ex1p, ex2p, ex3p, and ex4p) all used algebraic multigrid methods. MFEM also supports geometric ($h$- and $p$-multigrid) methods.

• These solvers are illustrated in Example 26 (and its parallel variant); see the ex26.cpp and ex26p.cpp source files.

• Mesh refinement can be set using the --geometric-refinements (-gr) command line argument.

• The finite element order can be controlled using the --order-refinements (-or) command line argument.

• This example runs matrix-free using MFEM's partial assembly algorithms. Matrix-free methods are much more efficient for high-order problems and also work better on GPU architectures.

• Try comparing the performance of ex1p and ex26p for higher-order problems. For example, compare the run time of the following two runs:

  mpirun -np 32 ./ex26p -m ../data/fichera.mesh -or 2
  mpirun -np 32 ./ex1p -m ../data/fichera.mesh -o 1
  

• Both examples solve a degree-4 Poisson problem with 1,884,545 degrees of freedom, but one of them is significantly faster.

• Explore how the number of CG iterations changes as -or and -gr are increased. (For large problems, it may be worth running ex26p in parallel with mpirun.)

  Low-order-refined methods